Abstract. The source of variability in the interval between action potentials has been identified in a class of cat spinal motoneurons. The observed random fluctuations in membrane potential (synaptic noise) together with an empirical description of spike generation accurately predict the statistical structure of variability observed to occur in the neuron's discharge.
The marked variability characteristic of most neurons' steady-state output has been of
considerable interest (1), because it has been believed to add uncertainty to the
information transmitted by the neuron and because it may provide clues about the
mechanisms underlying the transformation of input to output. Despite considerable
investigation, the sources of variability in the interval between action potentials (the
interspike interval) have not yet been clearly identified for any type of neuron. One
obvious possible source is the haphazard fluctuations in membrane potential (2) seen
even in the quiescent neuron. The question arises as to whether such input fluctuations
(synaptic noise) can account for the output (interspike interval ) variability. We have
shown that synaptic noise, together with a simple model for spike generation, can
indeed account for variability in the interspike interval in one class of cat spinal
motoneurons.
Intracellular recordings (Fig. 1) from spinal motoneurons suggest a mechanism by
which synaptic noise could produce variability in the interspike interval. During natural
stimulation, or when a constant current is passed through the recording electrode, many
previously silent spinal motoneurons discharged repetitively. Immediately after a spike
the membrane repolarizes, and then the membrane potential rises approximately
linearly to the firing level where another spike is generated (Fig. 1B). Superimposed
upon this ramp-like approach of the membrane potential to the firing level, however, are
random voltage fluctuations that look much like the synaptic noise of the quiescent
neuron. These fluctuations in voltage appear to cause the membrane potential to reach
the firing level at randomly varying times instead of at a fixed time, as would be the
case if no fluctuations were present. According to this model then, synaptic noise
produces variability in the inter spike interval by causing variations in the time at which
the membrane potential first crosses the firing level.
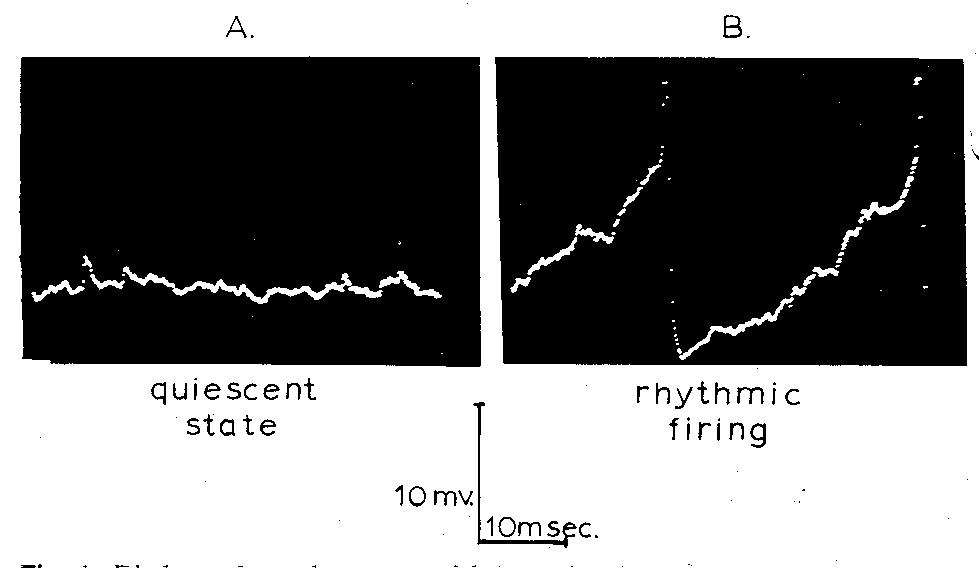
Fig. 1. Displays of membrane potential as a function of time showing
synaptic noise in a quiescent motoneuron (A) and the ramp-like approach
to the firing level with superimposed noise (B) when repetitive firing was
induced by current passed through the membrane. Note that the action
potentials are off scale in B. Because these records are displays of
digitalized data from LINC memory, the separate data samples are visible
as dots where the membrane potential was changing rapidly.
.
Although data from intracellular recordings are in qualitative agreement with our
proposed model, only quantitative evidence can establish that more complicated
assumptions are unnecessary. For example, it would be very difficult, on the basis of
mere inspection of records, to say that some source of noise other than synaptic noise
is not present, or that synaptic noise does not interact with the ramp generating
processes instead of simply adding to the membrane potential as it approaches the
firing level.
Specifically, then, we find that the statistical structure of variability in the interspike
interval can be accurately predicted from the observed properties of synaptic noise
together with a simple model of the spike-generating mechanism based on the assumption that the synaptic
noise simply adds to a linear rise of the membrane potential to a firing level.
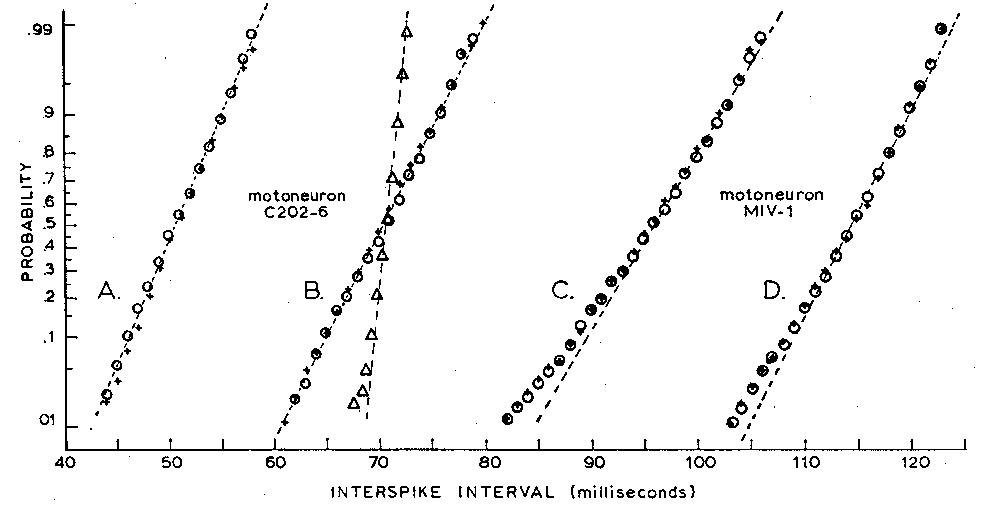
Fig. 2. Observed and predicted cumulative histograms of interspike
intervals from two motoneurons. The ordinate is a probability scale on
which a Gaussian distribution gives a straight line. Two sets of data from a
motoneuron whose firing level increased linearly with time after a spike are
shown (+) in (A) and (B), while results from a second motoneuron with a
constant firing level are shown (+) in (C) and (D). Predictions made from
synaptic noise and the observed characteristics of the spikegenerating
mechanism (open circles) are in good agreement with observed
histograms; if the time dependence of the firing level in (B) is ignored and if
a constant firing level is used for making the predictions, the predicted
points (open triangles) deviate markedly from the observed. For clarity of
the illustration, the points in (B) have been shifted 15 msec to the right
along the time axis.
Our data are based on observations of lumbosacral motoneurons in cats lightly anesthetized with
pentobarbital. Intracellular recordings were obtained with low-resistance (2 to 8 megohm) glass
microelectrodes filled with either 2.8M KCI or 2.5M potassium acetate. Signals were led through
a negative capacitance preamplifier, recorded on tape (frequency response flat from 0 to 5 khz),
and finally played back into a digital computer (LINC) for analysis. Analog voltages were
converted into eight-bit words with a sampling rate of 5 khz.
In the quiescent state all motoneurons exhibited the haphazard fluctuations in membrane
potential termed synaptic noise (Fig. 1A). When current was passed through the recording
electrode, the motoneuron fired repetitively (Fig. 1B), showing a ramp-like approach to the firing
level and prominent, superimposed fluctuations in membrane potential which have the same
appearance as synaptic noise seen in the resting neuron.
To analyze the interspike interval variability, we first compiled in the computer a list of intervals
between successive action potentials and screened these lists for segments of statistically
stationary data containing a minimum of 500 successive intervals. From about 100 neurons that
at the time of the experiment appeared to yield stable intracellular recordings, we have selected
four to report on here; seven segments of data from these four motoneurons were chosen for
detailed analysis.
Specifying completely the statistical structure of a neuron's interspike-interval variability would
require computation of the conditional probability of a particular interval length given the entire
past history of that neuron's behavior. For our motoneurons, however, serial autocorrelograms
revealed that an interval is independent of all preceding intervals; in this case, then, the
interspike-interval histogram provides a complete specification of a neuron's interval
fluctuations.
Cumulated interspike interval histograms from four lists of intervals yielded by two motoneurons
are shown in Fig. 2. These plots are made on a probability scale so that a Gaussian
interspike-interval histogram would give a straight line; histograms from cells not included in the
illustration were also approximately Gaussian [as opposed to exponential, multimodal, and so
forth (1)]
If the simple model of motoneuron behavior described earlier is accurate, we should be able to
predict these observed interspike-interval histograms from measurements on the synaptic noise
and on the average properties of the spike-generating mechanism by simulating motoneuron
behavior with the digital computer. Simulation is preferable to the analytic approach employed
earlier (4) because idealizing assumptions inapplicable to some neurons are thus avoided.
To make this simulation, a linearly rising "membrane potential" was generated in the computer,
and synaptic noise was added to this membrane potential ramp. When the membrane potential
plus noise first reached the "firing level," the length of time since the previous crossing of the
firing level was stored, and the membrane potential was reset to begin the process anew. In this
way, a sequence of "interspike intervals" could be generated, and their statistics could be
compared with those of the observed neuronal behavior.
Simulating a specific neuron's behavior requires that parameters be selected for the deterministic
spike-generation process and for the synaptic noise. The values for the ramp slope, starting point,
and firing level were measured from records of membrane potential. "Synaptic noise" for the
simulation was derived from one of two sources. In one instance the output of a commercial
whitenoise generator was filtered to produce noise with the same statistical structure (Gaussian
probability density and exponential autocorrelation function) as that observed in the neuron. In
the other cases, tape-recorded samples of synaptic noise from the quiescent cell were used.
Whatever the source of the noise voltage, it was sampled at 5 khz and added to the "membrane
potential" ramp generated within the computer. It must be emphasized that all parameters of the
simulation were estimated from intracellular recordings from the particular neuron whose
behavior was being examined and that a neuron's own synaptic noise was used in the simulation;
no parameters were obtained from the interspike-interval histograms we wished to predict.
Predicted interspike interval histograms for two motoneurons are shown in their cumulated form
in Fig. 2. The obviously good agreement between predicted and observed histograms was
confirmed by Kolmogorov-Smirnov goodness-of-fit tests (5); for all motoneurons included in
this report, more often than one time in five, two observed histograms generated by the
motoneuron itself would differ as much as the observed and predicted histograms.
The sensitivity of this method to inaccurate assumptions is illustrated by one of the cells
(C202-6) included in Fig. 2. Although the firing level was constant in some cells, it was observed
to increase linearly with time from the preceding spike in others. If this systematic rise in the
level was ignored--that is, if a constant firing level was adopted in the simulation--the predicted
interspike-interval histogram had a much smaller standard deviation than that observed for the
motoneuron (Fig. 2B). By arbitrarily increasing the amplitude of the synaptic noise in the
simulation by about 100 percent, we could make the predicted and observed standard deviations
of the interspike-interval histograms match; however, their shapes were different, the predicted
histogram being negatively skewed. When the increase in firing level (approximately 50
microvolt/msec) observed in the motoneuron was included in the simulation, the synaptic noise
seen in the cells gave an accurate prediction of the observed interspike-interval histograms
(circles, Fig. 2, A and B).
Although synaptic noise appears wellestablished as the dominant source of interspike-interval
variability in at least some cells, the question of whether additional noise sources make important
contributions in other cells naturally arises. This is a difficult question to answer, however, since
any failure to predict accurately the observed interspikeinterval histogram does not imply that
sources of variability other than synaptic noise were the cause of failure. For example, if the
firing level depends in some complicated way on the entire history of the membrane potential
path, that is, if voltage fluctuations that do not cross the firing level still have some effect on the
state of the neuron, then our predictions will fail because the model of the (deterministic)
spike-generating mechanism is inadequate and not because something other than synaptic noise
is a major source of noise. To identify a second major noise source, then, it must be shown ,that
including its observed properties in the stimulation leads to accurate prediction of the interspike
interval histogram. In one cell, we found the slope of the membrane potential ramp to vary
randomly from interval to interval. Since including this additional observed behavior in the
simulation leads to accurate prediction of the interspike-interval histogram, we have discovered
at least one instance where a source other than synaptic noise (presumably variability arising in
the spike-generating mechanism) is important. It is interesting to note that we have not yet found
neurons in which threshold variability has appeared to contribute significantly to the
interspike-interval variability.
WILLIAM H. CALVIN
CHARLES F. STEVENS
Department of Physiology and Biophysics,
University of Washington School of Medicine,
Seattle 98105
References and Notes
1. G. P. Moore, D. H. Perkel, J. P. Segundo, Annu. Rev. Phvsiol. 28, 493 (1966).
2. L G. Brock, J. S. Coombs, J. C. Eccles, J. Physiol. 117, 431 (1952); B. Katz and R. Miledi,
ibid. 168, 389 (1963); R. Granit, J. O. Kellerth, T. D. Williams, ibid. 174, 435 (1964); T. G.
Smith, Jr., Proc. Annu. Conf. Eng. Med. Biol. 18th 7, 120 (1965); R. E. Burke and P. G. Nelson,
Science 151, 1088 (1966); S. Watanabe and O. D. Creutzfeldt, Exp. Brain Res. 1, 48 (1966); S.
Hill, C. E. Polkey, T. D. Williams, in Muscular Aflerents and Motor Control, R. Granit, Ed.
(Wiley, New York 1966), p. 3630.
3. We thank Drs. J. W. Woodbury and A. M Gordon for the use of their LINC.
4. W. H. Calvin and C. F. Stevens, Proc. Annu. Cont. Eng. Med. Biol. 18th 7, 118 (1965).
5. D. A. Darling, Ann. Math. Stat. 28, 823 (1957).
6. This work was supported by NIH grant NB 05934. Computer facilities used were supported by
NIH grant FR 00150.
3 January 1967
mail@williamcalvin.com
|| Home Page || Calvin
publication list || My Science Surf
column || The
Calvin Bookshelf || scan and web, 7 Jan 97


