William H. Calvin University of Washington Box 351800 Seattle WA 98195-1800 USA Email || Home Page || publication list |
as it appeared in copyright ©1973 by authors and publisher. |
William H. Calvin University of Washington Box 351800 Seattle WA 98195-1800 USA Email || Home Page || publication list |
as it appeared in copyright ©1973 by authors and publisher. |
Equivalence of synaptic and injected current
_ ~ Elsevier Scientific Publishing Company, Amsterdam -Printed in The Netherlands
PETER C. SCHWINDT and WILLIAM H. CALVIN
Department of Physiology and Biophysics and of Neurological Surgery, University of Washington School of Medicine, Seattle, Wash. 98195 (U.S.A.)
Rhythmic firing in cat spinal motoneurons may be induced either by sustained synaptic input1 or by a constant current injected through the recording microelectrode l2. Differences in rhythmic firing behavior under sustained synaptic input as compared to injected current would suggest that the mechanisms underlying rhythmic firing are sensitive to the magnitude and perhaps the spatial distribution of the conductance changes accompanying sustained synaptic input. In many cases, sustained synaptic input and injected current seem to be equivalent in determining the overall input-output relation of the cell: added synaptic input may shift the plot of firing frequency versus injected current (the f-I curve) along the current axis as if the synaptic current simply added to (or subtracted from) the injected currents 9. On the other hand, synaptic input from supraspinal stimulation sometimes alters the slope of the f-I curvel3 l8 l9, and a recent theoretical investigational indicated that an f-I slope alteration should be seen when certain types of synaptic input are added.
The membrane potential between spikes (the 'trajectory') provides a more direct indication of the events underlying rhythmic firing than the f-I curve. Our recent studies l7 have shown that 3 types of trajectory change, each corresponding to a segment l2 of the f-I curve, may be seen when firing rate is altered by injected current alone. Even if it did not change the f-I curve slope, added synaptic input might result in different trajectory behavior, indicating a dependence of the mechanisms underlying rhythmic firing on the mode of driving current application or on the associated synaptic conductance changes. To test this possibility, the behavior of the membrane potential between spikes was examined during rhythmic firing with and without added synaptic input.
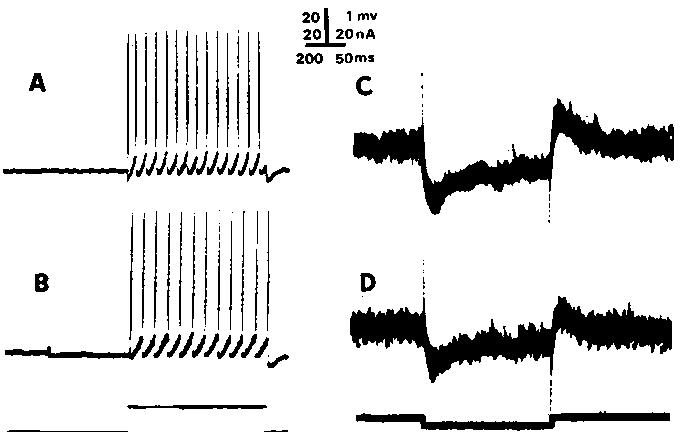
Fig. 1. Effect on rhythmic firing of a sustained synaptic input with net hyperpolarizing effect. A and B show rhythmic firing to a 15 nA step of current injected through the recording Microelectrode. In B. the injected current response is conditioned by a sustained synaptic hyperpolarization (starting at artifact) elicited by high frequency continual stimulation of a hindlimb nerve; the injected current then results in a lower firing rate (see Fig. 2A). In C and D, the input resistance shows a reduction to about 60 % of control levels (C) during sustained synaptic input (D). Five superimposed responses are shown; artifacts are capacitive bridge transients (bridge was balanced by spike height and firing level criteria). Response is to--5 nA pulse. Spikes retouchedExperimental and data processing methods have previously been described3 5-7 lfi. Cats were anesthetized with pentobarbital (35~0 mg/kg) and paralyzed with gallamine triethiodide. Rhythmic firing was produced by injecting constant current through the recording Microelectrode and, in 14 cells from 6 cats, various levels of depolarizing and hyperpolarizing synaptic currents were added prior to the injected current. Such sustained synaptic currents were produced by muscle stretch, continuous high frequency stimulation of various hindlimb nerves or, in a few cases, by bipolar stimulation in the region of the red nucleus. The procedure, as shown in Fig. 1B, was to apply the conditioning synaptic input, wait until the membrane potential reached a steady depolarization or hyperpolarization, and then to apply a constant step of injected current. Only adapted firing rates and trajectories (over the last 0.5 see of current injection) were considered. In the course of a larger study on rhythmic firing it was found that the f-I curve (Fig. 2A) itself could change during the course of an experimentl6; thus, the f-I slope in the present study was interpreted with care and referred to a stabilized value.
In the present study the added synaptic input did not produce a change in the f-I curve slope when only an increased 'synaptic noise' accompanied the change in membrane potential produced by the synaptic input. Random synaptic noise should itself have little effect on the primary rangers f-I curve slopers, but it was observed a few times that large, discrete EPSPs or IPSPs synchronous with nerve stimulation could change the f-I curve slope simply because the PSP size and timing in relation to the rhythmic firing frequency caused earlier-than-normal spikes or inhibited normal rhythmic spikes during the interspike intervals, i.e., not because the synaptic input changed the average trajectory behavior at a given firing frequency. When the effect of the synaptic input was simply to shift the f-I curve as for the illustrated cell, the magnitude of the synaptic current was inferred from the amount of the f-I curve shift (Fig. 2A) in terms of equivalent injected current.
Probably because of the pentobarbital anesthesia employed during these experiments, the added synaptic input was seldom able to produce rhythmic firing by itself. The maximum synaptic current obtained was usually equivalent to ~ 5 nA of injected current (as inferred from the lateral shifts of the f-I curves). Such an inference is reasonable only when, as in the present experiments, the increased synaptic noise is not too great7 16. Nevertheless, this synaptic current makes up a sizable fraction of the total driving current in the primary ranges; e.g., for the illustrated cell, the synaptic current provides 50 % of the total driving current at the minimum rhythmic firing rate, and 17% of the total at the total transition to secondary range; it is representative of the contribution of synaptic current obtained in all of the cells analyzed. Thus, if synaptic input produces significantly different trajectory behavior than injected current, this should be apparent under the synaptic input strengths used here, especially at the lowest firing rates. However, in all cells analyzed, the trajectories at a given firing rate were identical (within a maximum measuring error of 10%) with and without the added synaptic input.
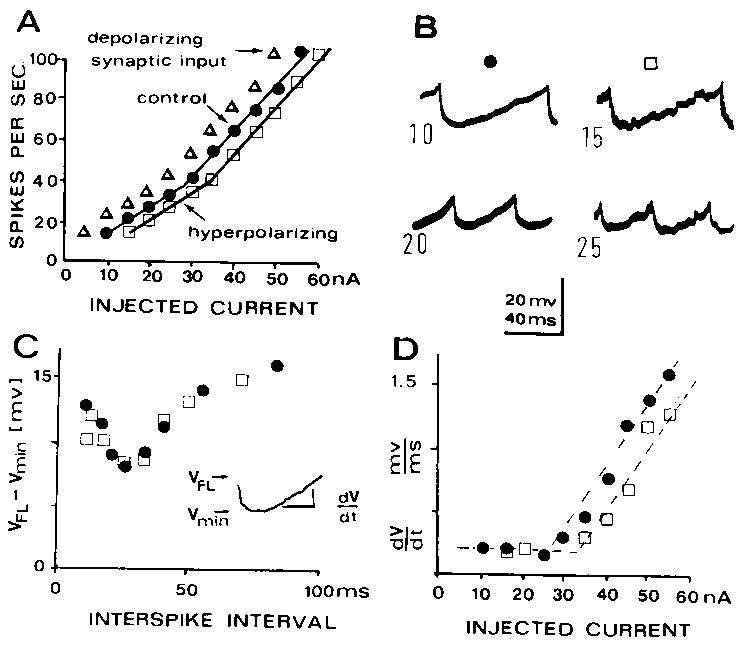
Fig. 2. Analysis of excitatory and inhibitory synaptic input upon rhythmic firing to injected current. Same motoneuron and same hyperpolarizing synaptic input as in Fig. 1. A: frequency-current (f-I) curve showing adapted firing rate plotted against Microelectrode current. This motoneuron develops a steeper f-I slope (secondary range) starting at about 35 spikes/sec. Control curve is shown by filled circles. Hyperpolarizing synaptic input (open squares) shifts the f-I curve to the right, as if the synaptic current could be countered by 5 nA of injected current at every Bring rate. Depolarizing synaptic currents (triangles) similarly shift the f-I curve to the left, as if they substituted for 5 nA of injected current. B: membrane potential trajectory between rhythmic spikes, corresponding to indicated injected currents. C and D: plots of trajectory descriptive parameters (defined by the inset in C) for control and hyperpo]arizing synaptic input conditions. Despite the reduction of resting input resistance to 60% of control values (Fig. 1D), the membrane potential trajectories do not change for a given firing rate. In C the range of the subthreshold excursion of the trajectory (VFL--Vmin) decreases during the primary range but increases for interspike intervals corresponding to the secondary range; this relation is not changed by the synaptic inputs. The ramp-like approach to firing level does not change slope in the primary range (foot of curve in D). In the secondary range the rate of rise to firing level increases and hyperpolarizing synaptic currents shift this relation to the right (upper part of curve in D). Trajectory parameters correspond to control values when correction is made for net synaptic current as determined by lateral shifts of the f-I curve. Similar results were obtained for depolarizing synaptic input (not shown).As seen in Fig. 2A, the added synaptic input produced a lateral shift of the f-I curve of ~ 5 nA. Since the injected current itself was also incremented by 5 nA each time, the trajectories (Fig. 2B) due to injected current alone (filled circles) can be compared with conditioned trajectories for the same firing rate. Such comparison indicates that superposition of the trajectories is possible. Further confirmation of identical trajectory behavior can be obtained by comparison of various measures of trajectory shaped shown in the inset for Fig. 2C. Points in Fig. 2C and D are for averages over 5-15 trajectories; these trajectory parameter plots have been shown to be appropriate quantitative descriptions of trajectory shapes and trajectory changes with firing rate; differences of 10% are easily detected. The plots of maximum trajectory excursion below firing level versus interspike interval (Fig. 2C) are identical with and without added synaptic input. The plots of depolarization rate versus the current (Fig. 2D) also are identical with and without added synaptic input when the appropriate correction is made for net synaptic current. The maximum variation in individual points is about 5 ~ with and without added synaptic input and the variation appears to be random. Such trajectory parameter plots were also used to compare trajectory behavior when the synaptic current was not equal to the 5 nA injected current increments.
When depolarizing synaptic input was added, there was usually no significant change in the cell input resistance (not shown) which may indicate that most of the synaptic conductance change was remote from the soma15. Hyperpolarizing synaptic input usually decreased the input resistance, sometimes to approximately 60% the rest value as in Fig. 1D, suggesting that most of the synaptic input was near to the soma. While this is consistent with the locations inferred for excitatory10 l5 and inhibitory2 group la input respectively, other pathways besides group Ia may also be activated with sustained input.
The invariance of the trajectory behavior with or without synaptic input providing up to 50% of the total driving current and under different spatial distributions of synaptic input suggests that the motoneuron is not sensitive to the mode of driving current application nor its spatial distribution, and that current injected into the soma gives an accurate representation of trajectory behavior during rhythmic firing. In the present study, synaptic stimulation of supraspinal structures13 In 19 gave the same results in the few cases studied.
Not only does the trajectory (and f-I curve) behavior seem independent of the mode of driving current application, but there seem to be no significant trajectory alterations for a given firing rate (Fig. 2B-D) even when the resting input resistance has been reduced 40% by the synaptic inputs (Fig. 1D). This suggests that soma conductance component dominates the trajectory behavior: if the active conductance throughout the interspike interval is small compared to the channel provided by passive dendrites, perhaps a further increase in the dendritic route due to increased synaptic conductances would produce little change in the already small current flowing through active channels. A more likely explanation is that the active conductances during rhythmic firing are large enough compared to the passive conductances that even the increased synaptic conductance does not divert significant amounts of applied current away from the active membrane. In the absence of the active trajectory-producing conductances in the subthreshold region around the resting potential, the increased synaptic channels significantly divert applied currents, and reduce the depolarization produced by a small current pulse 1as in Fig. 1D).
Kernell's theoretical studyl4 predicts f-I slope changes for his 'D type' cells under excitatory dendritic input; such f-I slope changes (or at least the more sensitive indicator, alterations in trajectory behavior), should have been measurable in our experiments for depolarizing synaptic input. However, no attempt was made here to provide dendritic inhibition, which Kernell predicted to produce the maximum increase of the f-I curve slope. Kernell's theoretical predictions depend on the spatial distribution of both the synaptic conductances and the active conductances underlying rhythmic firing, and these appear to be somewhat different than assumed in Kernell's model14.
The change in input resistance which may accompany steady synaptic drive upon a cat spinal motoneuron is known to reduce the amplitude and decay time constant of monosynaptic EPSPs20, thus, whether an input is depolarizing or hyperpolarizing, it may have an 'inhibitory' effect on other inputs, in the sense that greater currents are now required to produce a depolarization which will reach threshold and elicit an action potential. While such conductance changes due to sustained synaptic input may produce changes in the efficacy of other inputs (whether PSPs or injected current) for reaching threshold from rest, they need not have such a shunting effect once the inputs are sufficient to produce rhythmic firing; only the net driving current, however applied, seems to be important in the rhythmic firing mode.
We thank Jerrold Maddocks for his technical assistance.
1. BURKE, R. E., Firing patterns of gastrocnemius motor units in the decerebrate cat, J. Physiol. (Lond.), 196 (1968) 631-654.
2 BURKE, R. E., FEDINA, L., AND LUNDBERG, A., Spatial synaptic distribution of recurrent and group Ia inhibitory systems in cat spinal motoneurones, J. Physiol. (Land.), 214 (1971) 305-326.
3 CALVIN, W. H., Evaluating membrane potential and spike patterns by experimenter-controlled computer displays, Exp. Neurol., 21 (1968) 512-534.
4 CALVIN, W. H., Synaptic potential summation and repetitive firing mechanisms: input-output theory for the recruitment of neurons into epileptic bursting firing patterns, Brain Research, 39 (1972) 71-94.
5 CALVIN, W. H., Computer-based 'kymograph' for photographing raw neurophysiological data, J. appl. Physiol., 34 (1973) 133-135.
6 CALVIN, W. H., AND SCHWINDT, P. C., Steps in production of motoneuron spikes during rhythmic firing, J. Neurophysiol., 35 (1972) 297-310.
7 CALVIN, W. H., AND STEVENS, C. E., Synaptic noise and other sources of randomness in motoneuron interspike intervals, J. Neurophysiol., 31 (1968) 574-587.
8 GRANIT, R. KERNELL, D., AND LAMARRE, Y., Algebraical summation in synaptic activation of motoneurones firing within the 'primary range' to injected currents, J. Physiol. (Lond. J,187 (1966) 372-399.
9 GRANIT, R., KERNELL, D., AND LAMARRE, Y., Synaptic stimulation superimposed on motoneurons firing in the 'secondary range' to injected current, J. Physiol. fLond), 187 (1966) 401-415.
10 JACK, J. J. B., MILLER, S., PORTER, R., AND REDMAN, S. J., The time course of minimal excitatory post-synaptic potentials evoked in spinal motoneurones by group IA afferent fibers, J. Physiol. (Lond.), 215 (1971) 353-380.
11. KERNELL, D., The adaptation and the relation between discharge frequency and current strength of cat lumbosacral motoneurones stimulated by long-lasting injected currents, Acta Physiol. scand., 65 (1965) 65-73.
12 KERNELL, D., High-frequency repetitive firing of cat lumbosacral motoneurones stimulated by long-lasting injected currents, Acta Physiol. scand., 65 (1965) 74 86.
13 KERNELL, D., Synaptic influence on the repetitive activity elicited in cat lumbosacral motoneurons by long-lasting injected currents, Acta Physiol. scand., 63 (1965) 409 410.
14 KERNELL, D., Effects of synapses on dendrites and soma on the repetitive impulse firing of a compartmental neuron model, Brain Research, 35 (1971) 551-555.
15 RALL, W., BURKE, R. E., SMITH, T. G., NELSON, P. G., AND FRANK, K., Dendritic locations of synapses and possible mechanisms for the monosynaptic EPSP in motoneurons, J. Neurophysiol., 30 (1967) 1169-1193.
16 SCHWINDT, P. C., Membrane-potential trajectories underlying motoneuron rhythmic firing at high rates, J. Neurophysiol., 36 (1973) 431 449.
17 SCHWINDT, P. C, AND CALVIN, W. H., Membrane-potential trajectories between spikes underlying motoneuron firing rates, J. Neurophysiol., 35 (1972) 311-325.
18 SHAPOVALOV, A. I., AND GRANTYN, A. A., [Suprasegmental synaptic influences on chromatolysed motor neurones], Biofizika, 13 (1968) 260 269.
19. SHAPOVALOV, A. I., Extrapyramidal monosynaptic and disynaptic control of mammalian alphamotoneurons, Brain Research, 40 (1972) 105-116.
20 TERZUOLO, C. A., LLINAS, R. AND THOMAS GREEN, K., Mechanisms of supraspinal actions upon spinal cord activities, Arch. ital. Biol.., 103 (1965) 635-651.