|
A book by William H. Calvin UNIVERSITY OF WASHINGTON SEATTLE, WASHINGTON 98195-1800 USA |
|
HOW BRAINS THINK
A Science Masters book (BasicBooks in the US; to be available in 12 translations) copyright ©1996 by William H. Calvin |
|
Shaping up an Intelligent Act from Humble Origins
Is this chapter really necessary? Well, no — in the sense that many people could skip to the last chapter without realizing that something was missing. It all depends on how satisfied you are with organization charts. Some people don’t want to know any more. “Skip the details,” they say, “and just stick with the executive summary.” But this chapter really isn’t about the details omitted from the last chapter — it’s written from a different perspective, bottom-up rather than inferred principles. Principles are, unfortunately, rather like organization charts — a sketchy, convenient fiction. Real organizations have a flow of information and decision making that isn’t captured by the boxes and labels. Charts fail to take account of people and how they talk to one another, fail to take account of the “institutional memory.” They fail to take account of how experts can also be generalists, of how decisions taken at one level interact with those taken at another. Any schematic account of the brain will share the shortcomings of organization charts. This account of intelligence has, so far, failed to take much account of neurons — the nerve cells of the brain — and how they talk to one another, how they remember past events, how they collectively make decisions on a local and regional scale. Some of that simply isn’t known yet, but it is certainly possible to sketch out a plausible account of copying competitions among the cerebral codes. Whenever you are talking science, a good general rule is always to give a specific example — even if it is only a possible mechanism rather than a well-established one. That’s what this chapter provides: an example of how our cerebral cortex might function as a Darwin Machine and, in the process, create that constantly shifting focus of consciousness, even those subconscious thoughts that every so often pop into the foreground, unbeckoned. It shows how we might achieve the offline ability to simulate our future actions in the real world — an ability that is the essence of guessing-right intelligence. The inability to imagine a mechanism that could produce mind is at the heart of many of the Janitor’s Dream and the mind-in-a-computer objections. This chapter describes the building blocks with which I can imagine how a thinking machine could be constructed. Your mileage may vary — but here’s your chance, just one chapter long, to see a bottom-up mechanistic example of how our mental lives might operate, both consciously and subconsciously, both for the novel and the routine.
|

Gray matter isn’t really gray, except in a dead brain; in a living brain, it’s got a rich blood supply. Think of those rivers that run reddish-grayish-brown after a thunderstorm, and you’ll have the right hue for the dynamic “gray matter.” The white matter in the brain, however, is really white, a porcelain hue, because of the fat that insulates the long, stringy part of a neuron. This part, which is called the “axon,” is analogous to a wire and carries the neuron’s output signal to near and distant targets. “Myelin” is the proper name for its fatty insulation. White matter is simply wire bundles, going every which way, much as you would see in the basement of a telephone-central office building. The bulk of the brain is insulated wires connecting the parts that do the hard work, which are far smaller. At one end of the axon is the neuron’s cell body, the globular part of the cell containing the nucleus, with the DNA blueprints for the cell’s day-to-day operation and maintenance. There are lots of treelike branches, called dendrites, arising from the cell body. Because cell bodies and dendrites lack the white insulation, large collections of them look “gray.” The far end of a neuron’s axon appears to be touching the dendrite of a downstream neuron — though, if you look carefully with an electron microscope, you’ll see a little gap between the two cells, called a synapse. Into this no-man’s-land the upstream neuron releases a little neurotransmitter, which drifts across the gap and opens up some channels through the membrane of the downstream neuron. (Though there are some retrograde neurotransmitters in addition, a synapse is usually a one-way street, so it’s useful to refer to “upstream” and “downstream” neurons.) Overall, a single neuron looks like a bush, or the root of some herb such as ginger. It is the typical unit of computation, summing up the influences of a few thousand inputs — most of them excitatory, and some of them inhibitory, like deposits and checks — and speaking, in a single voice, to several thousand hardwired listeners. The message sent from this “checking account” mostly concerns its “account balance” and how fast that balance is increasing. No message is sent unless the balance exceeds some threshold. Big deposits generate big messages, like interest payments with a bonus. But, just as piano keys don’t produce any sound unless struck hard enough, cortical neurons are usually silent unless input conditions are surging — and then their output is proportional to how much they’re stimulated by that account balance. (Oversimplified binary models usually treat a neuron as more like a harpsichord key, with a threshold but no gradation in volume for harder hits.) Though the messages from short neurons can be simpler, neurons with axons longer than about 0.5 mm always utilize a signal booster: the impulse, a brief up-and-down voltage change of a standard size (like the loudness of that harpsichord key). Amplified and fed into a loudspeaker, the impulse sounds like a click (and we talk of the neuron “firing”). To get around the standard-size limitation, impulses usually repeat at a rate proportional to the account balance, the same way that a few quick repetitions of a harpsichord note may imitate a hard-struck piano note. Sometimes — especially in cerebral cortex — just a few inputs, out of thousands, can conspire to trigger an impulse.
|
|
The really interesting gray matter is that of the cerebral cortex, because that’s where most
of the novel associations are thought to be made — where the sight of a comb, say, is matched up
to the feel of a comb in your hand. The cerebral codes for sight and feel are different, but they
become associated somehow in the cortex, along with those for hearing the sound /km/ or
hearing the characteristic sounds that the tines of a comb make when they’re plucked. You can,
after all, identify a comb in any of these ways. It’s hypothesized that there are specialized places
in the cortex, called “convergence zones for associative memories,” where those different
modalities come together. On the production side, you have linked cerebral codes for pronouncing /km/ and for generating the movements that manipulate a comb through the hair on your head. So between the sensory version of the word “comb” and the various movement manifestations, we expect to find a dozen different cortical codes associated with combs. The cortical areas that do all this associating for us are a thin layer of icing on the cake of the white matter. The cerebral cortex is only about 2 mm thick, though it is deeply wrinkled. The neocortex (which is all of cerebral cortex except for hippocampus and some of the olfactory areas) has a surprisingly uniform packing density (with the exception of one layer of the primary visual cortex). If you made a grid atop the cortical surface, each square millimeter would have about 148,000 neurons beneath it — whether it was language cortex or motor cortex. But a sideways look, at the layers within that 2 mm depth, reveals some regional differences. It’s the icing of this cake that contains the layers, not the cake itself. A better bakery analogy might be a flaky pie crust made of croissantlike layers. The deepest layers are like an out box, their wires mostly heading out of the cortex, bound for distant subcortical structures, such as the thalamus or the spinal cord. The middle layer is an in box, with wires arriving from the thalamus and other such places. The superficial layers are like an interoffice box; they make “corticocortical” connections with the superficial layers of other regions, both adjacent and distant. It’s their axons that go through the corpus callosum to the other side of the brain — but most of the interoffice mail is delivered locally, within several millimeters. Such axon branches run sideways, rather than detouring through the white matter like the longer “U-fiber” branches. Some regions have big in boxes and small out boxes, just like the ones to be found on the editorial-department desk that deals with letters to the editor. Superimposed on this stacked horizontal organization, moreover, is a fascinating set of vertical arrangements, similar to newspaper columns. |
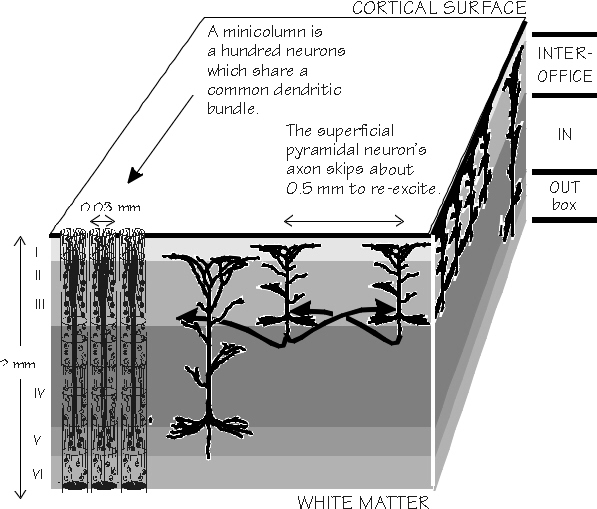
If we go around wiretapping the individual neurons in the cerebral cortex, we discover that neurons with similar interests tend to be vertically arrayed there, forming cylinders known as cortical columns, which cut through most of the layers. It’s almost like a club that self-organizes out of a crowd at a party, where people of similar interests tend to cluster together. We have naturally given names to these cortical clubs. Some of the names reflect their size, some their seeming specialties (so far as we know them). The thin cylinders, or minicolumns, are only about 30 m in diameter (that’s a very thin hair, closer to the threads of a spider web). The best-known examples of these are the visual cortex’s orientation columns, whose neurons seem to like visual objects with a line or border tilted at a particular angle. The neurons in one minicolumn will respond best to boundaries tilted at 35, those in another will like horizontals or verticals, and so forth. You can look in a microscope and see (well, it takes some doing, even after a century of progress in neuroanatomical technique) a group of cortical neurons bundled together like stalks of celery. There is a tall “apical dendrite” that stretches up toward the cortical surface from the cell body (which is often triangular in appearance, hence the name “pyramidal neuron”). It is those apical dendrites of the pyramidal neurons that are bundled together, with 30 m between adjacent bundles. There are about 100 neurons in a minicolumn organized around one of those bundles, though the bundle at any one level might only have a dozen apical dendrites in it. Bundling is a commonplace outside visual cortex, so minicolumns are likely a common element of cortical organization, just from the anatomy — but elsewhere we are ignorant of what the neurons of a minicolumn are “interested in.” Other “interest groups” tend to be much larger and comprised of more than a hundred minicolumns; these so-called macrocolumns are 0.4-1.0 mm across (that’s a thin pencil lead) and sometimes appear more like elongated curtain folds than like proper cylinders. Such macrocolumns seem to result from an organization of the inputs — for example, in visual cortex those axons carrying information from the left eye tend to alternate every 0.4 mm with those being relayed from the right eye. Inputs from other parts of the cortex itself tend to do the same thing; for example, looking at the cortical area just in front of the corpus callosum, you can see the inputs from the prefrontal cortex forming a macrocolumn, flanked on either side by macrocolumns formed by a clustering of parietal-lobe inputs. The cortical neurons interested in color tend to cluster together (though not exclusively) in “blobs.” Unlike macrocolumns, blobs don’t extend through all layers of the cortex; they’re found only in the superficial layers — up there with the interoffice mail. And they’re not exclusively comprised of color specialists: perhaps only 30 percent of the neurons in a blob are color sensitive. The distances between blobs are similar (if not identical) to the those of the macrocolumns.
|
|
Next level of organization? On the basis of layer thickness changing, there are 52
“Brodmann Areas” in each human hemisphere. At a boundary between Areas, you’ll see the
relative thickness of those interoffice-in-out stacked boxes change, as if the relative amounts
of incoming, outgoing, and interoffice mail differed on adjacent “desks.” Area 17 is better known as the primary visual cortex, but generally it is premature to put functional labels on these areas in the manner of departments on an organization chart (Area 19, for example, has a half-dozen functional subdivisions). A Brodmann Area averages 21 cm2 in unwrinkled area. If the visual cortex ratio holds elsewhere, that’s on the order of 10,000 macrocolumns and a million minicolumns in the average cortical area. That factor of a hundred keeps recurring. a hundred neurons to a minicolumn, roughly a hundred minicolumns to a macrocolumn, a hundred times a hundred macrocolumns to a cortical area (which makes me wonder if we’re missing an intermediate “super-column” or “mini-area” organization on the scale of a hundred macrocolumns), and there are just over a hundred Brodmann Areas, when you total those in both cerebral hemispheres. Can we extend this hundred-fold multiplier further? It does put us into the scale of social organizations: What’s a hundred brains? That suggests certain legislative bodies such as the U.S. Senate. And the United Nations is representative of more than a hundred legislatures.
|
|
Permanent elements of brain organization, such as cortical areas or minicolumns, are nice to know about. But we also need to understand those temporary work spaces of the brain — something closer to scratch pads and buffers — that are likely superimposed on the more permanent forms of anatomical organization. To deal with the novel, we are indeed going to need some empirical types of organization, like those hexagonal cells that form in the cooking oatmeal when you forget to stir it — forms that are used temporarily and then disappear. Occasionally these forms of organization are recalled to life if some aspect of them earlier formed enough “ruts” in the landscape of interconnection strengths — in which case the empirical organization became a new memory or habit. In particular, we need to know about the cerebral codes — those patterns that represent each of the words of our vocabulary, and so forth — and what creates them. At first, it appears that we are dealing with a four-dimensional pattern — the active neurons scattered through three-dimensional cortex, as they perform in time. But largely because the minicolumns seem to organize all the cortical layers around similar interests, most people working on cortex think of it as a two-dimensional sheet, rather like the retina (yes, the retina is 0.3 mm thick and is subdivided into a few layers, but the mapping is clearly for a two-dimensional image). So we can try thinking of two dimensions, plus time, for cortex (which is, of course, the way we apprehend the images on a movie screen or computer terminal) — perhaps with transparent overlays when the different cortical layers do different things. Just imagine the human cortex flattened out on those four sheets of typing paper like pie crust, with little patches lighting up like message-board pixels. What patterns will we observe when that cortex is seeing a comb? When the word “comb” is heard, or said? When the cortex is commanding a hand to comb the hair? Memory recall may consist of the creation of a spatiotemporal sequence of neuron firings — probably a sequence similar to the firing sequence at the time of the input to memory, but shorn of some of the nonessential frills that promoted it. The recalled spatiotemporal pattern would be something like a message board in a stadium, with lots of little lights flashing on and off, creating an overall pattern. A somewhat more general version of such a Hebbian cell assembly would avoid anchoring the spatiotemporal pattern to particular cells, to make it more like the way the message board can scroll. The pattern continues to mean the same thing, even when it’s implemented by different lights. Though we tend to focus on the lights which turn on, note that lights that stay off also contribute to the pattern; if they are turned on randomly — by seizures, for example — they fog the pattern. Something similar to this fogging seems to happen in concussions: while an injured football player is being helped off the field, he can often tell you what play he was running, but ten minutes later he can’t remember what happened to him. Injury slowly causes a lot of neurons to “light up,” and patterns therefore become obscured in the manner of bright fog — what mountain climbers call “whiteouts.” (Just remember: blackouts are sometimes from whiteouts.)
|
|
What’s the most elementary pattern that means something? A major clue, it seems to
me, is that pattern copying is needed, for various reasons. Before DNA leapt to prominence, geneticists and molecular biologists were searching for a molecular structure that was capable of being reliably copied during cell division. One of the reasons that the double helix structure was so deeply satisfying when it was discovered in 1953 by Crick and Watson (and I write this while temporarily at the University of Cambridge, just across the courtyard from the building where they worked) was that it provided a way of making a copy, via the complementary pairs of DNA bases (C bonds with G, A pairs with T). Unzip the double helix into two separate halves and each DNA position on a half zipper will soon be paired with another of its opposite type, just from all the loose ones floating around in the nucleotide soup. This gives you two identical double helices, where there was only one before. This copying principle paved the way for the understanding of the genetic code (how those DNA triplets “represented” the amino acid string that folds up into a protein) a few years later. Is there a similar copying mechanism for cerebral activity patterns, and might it help us identify the most relevant of the Hebbian cell assemblies? That’s the one that we could properly call the cerebral code because it is the most elementary way of representing something (a particular connotation of a word, an imagined object, and so forth). Copying hasn’t been observed in the brain yet — we don’t currently have tools of sufficient spatial and temporal resolution, though we’re close. But there are three reasons why I think it’s a safe bet.
The strongest argument for the existence of copying is the darwinian process itself, which is inherently a copying competition biased by a multifaceted environment. It’s so elementary a method for shaping up randomness into something fancy that it would be surprising if the brain didn’t use it.Since 1991, my favorite candidate for a local neural circuit that could make copies of spatiotemporal patterns has been the mutually reinforcing circuitry of the interoffice mail layers. The wiring of those superficial layers of cerebral cortex is, in a word, peculiar. Indeed, to a neurophysiologist, almost alarming. I look at those circuits and wonder how runaway activity is reined in, why seizures and hallucinations aren’t frequent events. But those same circuits have some crystallization tendencies that ought to be particularly good at cloning spatiotemporal patterns.
|
|
Of the hundred neurons in a minicolumn, about 39 are superficial pyramidal neurons (that is, their cell bodies reside in the superficial layers II and III). It’s their circuitry that is peculiar. Like all other pyramidal neurons, they secrete an excitatory neurotransmitter, usually glutamate. There’s nothing peculiar about glutamate per se; it’s one of the amino acids, more typically used as a building block of peptides and proteins. Diffusing across the synapse, the glutamate opens up several types of ion channels through the membrane of the next cell’s dendrite. The first channel specializes in letting sodium ions through; that in turn raises the internal voltage of the downstream neuron. A second downstream channel activated by glutamate is known as the NMDA channel, and it allows calcium ions into the downstream neuron along with some more sodium. NMDA channels are particularly interesting to neurophysiologists because they contribute to so-called long-term potentiation (LTP), a change in synaptic strength that endures for some minutes in neocortex. (Minutes, actually, is closer to the neurophysiological “short-term,” but LTP sometimes lasts days in the hippocampus — which is an older and simpler version of cortex — and that’s where the “long-term” name originated.) LTP occurs when there is near synchrony (within dozens to hundreds of milliseconds) of several inputs to the downstream neuron; it simply turns up the “loudness control” for those inputs for a few minutes. Those are the “bumps and ruts” that temporarily make it easier to re-create a particular spatiotemporal pattern. LTP is our best candidate for a short-term memory that can survive a distraction. It is also thought to contribute the scaffolding for the construction of truly long-lasting structural changes in synapses — the permanent bumps and ruts that aid in the re-creation of long-unused spatiotemporal patterns. The interoffice layers are where most of the NMDA channels are located, and where most of the neocortical LTP occurs. These superficial layers have two more peculiarities, both of them having to do with the connections that their pyramidal neurons make with one another. On average, a cortical neuron contacts fewer than 10 percent of all neurons within a radius of 0.3 mm. But roughly 70 percent of the excitatory synapses on any superficial-layer pyramidal neuron are derived from pyramidal neurons less than 0.3 mm away, so these neurons may be said to have an unusually strong propensity to excite one another. To a neurophysiologist, that raises all sorts of red flags: it’s a perfect setup for instability and wild oscillations, unless it’s carefully regulated. There is also a peculiar patterning to these “recurrent excitatory” connections — a patterning not seen in the lower cortical layers. The axon of a superficial pyramidal neuron travels sideways a characteristic distance without making any synapses with other neurons, and then it produces a tight terminal cluster. Like an express train, it skips intermediate stops. In the primary visual cortex, the distance from the cell body to the center of the terminal cluster is about 0.43 mm in primary visual cortex; next door in a secondary visual area, it’s 0.65 mm; in the sensory strip, it’s 0.73 mm; and in motor cortex of monkeys, it’s 0.85 mm. Let me, for convenience, just call this skip spacing a generic 0.5 mm. The axon may then continue for an identical distance and sprout another terminal cluster, and this express train line may continue for some mm. This skip-spacing is distinctly peculiar in the annals of cortical neuroanatomy. Its function is unknown, but it certainly does make you think that regions 0.5 mm apart might be doing the same thing on occasion — that there could be repeating patterns of activity, in the manner as recurring patterns within wallpaper.
|
|
The skip spacing, you may have noticed, is the same half-mm-or-so as the distance between
macrocolumns. Color blobs, too, are about that far apart from one another. Yet there’s a
difference. A second superficial pyramidal neuron 0.2 mm from the first will itself have an axon with different express stops, still at 0.5 mm skips but each cluster landing 0.2 mm from those of the first. In my undergraduate days, the Chicago Transit Authority had exactly such a system of A trains and B trains, one taking the “even” stops and the other the “odd” numbered ones, with a few common stops for transferring between trains. Of course, any one subway stop is sometimes stretched out over more than a city block — and our superficial pyramidal neurons are also not located at a single point, as their dendritic tree spreads sideways from the cell body, often 0.2 mm or more. Contrast this to macrocolumns. So far, they’ve been territories within which there is common source of input, as if you could draw a fence around a group of minicolumns on the basis of their all being on the same mailing list. And the blobs have an output target in common (secondary cortical areas specializing in color). So we’re not talking macrocolumns with our sideways-running excitatory axon branches, though perhaps the skip spacing is a cause (or effect) of the macrocolumns at an adjacent level of organization. Imagine a forest where tree branches interdigitate, where each tree has a telephone line leaving it and contacting a distant tree, not only bypassing the intermediate ones, but leaping over the common-input fences subdividing the forest. Sideways “recurrent” connections are common in real neural networks; lateral inhibition was the topic of two Nobel Prizes (to Georg von Békésy in 1961 and H. Keffer Hartline in 1967). It tends to sharpen up fuzzy boundaries in a spatial pattern (while they may compensate for fuzzy optics, they can also produces a few side effects, such as some of the visual illusions). But our superficial pyramidal neurons are excitatory to one another, suggesting that their activity could feed on itself like a spreading brushfire, unless held in check by inhibitory neurons. What’s going on here? Is recurrent excitation why the cerebral cortex is so prone to epileptic seizures, when the inhibitory neurons are fatigued? Furthermore, the standard skip-spacing means that a round trip might be possible — a reverberating circuit, of the kind postulated by early neurophysiologists. Two neurons that are 0.5 mm apart may keep each other going. A neuron has a refractory period — a kind of “dead zone” — after an impulse is produced: for a millisecond or so, it is almost impossible to initiate another impulse. The travel time over that 0.5 mm is also about a millisecond, and then the synaptic delay slows delivery by another half a millisecond — so if the connections between the two neurons were otherwise strong enough, you can imagine the second neuron’s impulse getting back to the first neuron about the time it has recovered its ability to generate another impulse. But usually connection strength between neurons isn’t strong enough, and usually such rapid firing cannot be kept up, even if it does get started. (In the heart, however, connection strengths between adjacent cells are indeed strong enough, and circus re-excitation is an important pathology when injury slows travel times.) If the implication of cortex’s standard skip-spacing isn’t an impulse chasing its tail, then what is it? Probably synchronization.
|
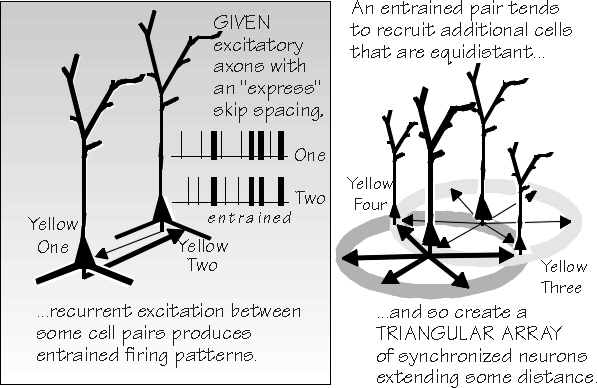
If you sing in the chorus, you get in sync with the others by hearing them — usually hearing yourself coming in too late or starting too early. But you, of course, are also influencing them. Even if everyone is a little hard of hearing, everyone soon gets synchronized, thanks to all that feedback. Your position in that chorus is very much like that of a superficial pyramidal neuron in the neocortex, getting excitatory inputs from neighbors on all sides. Networks like this have been extensively studied, even if the one in superficial neocortex has not; synchronization will occur even with only small amounts of feedback (which is why I postulated that you were hard of hearing, just then). Two identical pendulums will tend to synchronize if they are adjacent, just from the air and shelf vibrations they create. Menstrual cycles are said to synchronize in women’s dormitories. Though harmonic oscillators, such as the pendulums, take a while to get in sync, nonlinear systems, such as impulse production in neurons, can synchronize very quickly, even if the mutual connection strengths are relatively weak. And what does this tendency to synchronize have to do with copying spatiotemporal patterns? Happily, it’s all a matter of simple geometry, the kind that the ancient Greeks discovered while staring at the tile mosaics of their bathhouse floors (and that many of us have rediscovered in wallpaper patterns).
|
| SUPPLEMENTARY MATERIAL: There are now animated illustrations for the spatiotemporal patterns.
Let us suppose that a “banana committee” is forming, of all the superficial pyramidal
neurons scattered around the primary visual cortex that respond to one feature or another of the
banana you’re looking at. The lines forming the outline of the banana are a particularly effective
prod to those neurons that specialize in boundaries and their orientation. Then there are those
blob neurons that like yellow.
Since they tend to excite one another, given that 0.5 mm skip distance for their axon terminal
clusters, there is going to be a tendency for them to synchronize — not that all impulses in the
neuron I’ll call Yellow One will be synchronized with those in Yellow Two, but a certain
percentage will occur within a few milliseconds of one another.
Suppose now that there is another superficial pyramidal neuron, 0.5 mm equidistant from both
Yellow One and Yellow Two. Perhaps it only receives a weak yellow input, so that it isn’t
actively firing away, signaling yellow. Now, however, Yellow Three is getting inputs from both
One and Two. Furthermore, some of those inputs from One and Two — the synchronized ones —
will arrive at Three’s dendrites together. (They both have the same 0.5 mm travel distance.) This
is exactly what hi-fi buffs call “sitting in the hot spot,” equidistant from both speakers at the
apex of an equilateral triangle (move even slightly to either side and the stereo illusion collapses
into the nearest speaker, leaving you with mono sound). At the cortical hot spot near Three, the
two synaptic inputs summate, 2+2=4 (approximately). But the distance remaining to the impulse
threshold may be 10, so Three still remains silent.
Not very interesting. But these are glutamate synapses in the superficial cortical layers, so
they’ve got NMDA channels across the synapse to let both sodium and calcium into the
downstream neuron. Again, not so important — by itself.
But I temporarily omitted telling you why neurophysiologists find NMDA channels so
fascinating compared with other synaptic channels: they are sensitive not only to arriving
glutamate but also to the preexisting voltage across the postsynaptic membrane. Raise that
voltage and the next glutamate to arrive will cause a bigger effect, sometimes twice the standard
amount. This is because many of the NMDA channels are normally sitting there plugged up:
there’s a magnesium ion stuck in the middle of the tunnel through the membrane; increased
voltage will pop it out of there — and that in turn allows formerly blocked sodium and calcium to
flow into the dendrite on the next occasion when arriving glutamate opens up the gates.
The consequence of this is important: it means that synchronously-arriving impulses are more
effective than 2+2 would predict: the sum could be 6 or 8 instead (welcome to nonlinearity).
Repeated near-synchronization of two inputs is even more effective, as they clean the magnesium
plugs out of each other’s channels. Pretty soon, those repeatedly synchronous inputs from
Yellow One and Yellow Two might be able to trigger an impulse from Yellow Three.
Standard-distance mutual re-excitation and NMDA synaptic strength augmentation have this
interesting hand-and-glove fit, all because of the tendency to synchronize. Emergent properties
often come from just such combinations of the seemingly unrelated.
|
|
We now have three active neurons, forming the corners of an equilateral triangle. But there
might be a fourth, over on the other side of One and Two, also equidistant at 0.5 mm away.
There isn’t very much data yet on how many axon branches there are from a single superficial
pyramidal neuron — but looking down from the top, in one dye-filled and exhaustively
reconstructed superficial pyramidal neuron, showed branches in many directions. So there ought
to be a doughnutlike ring of excitation, about 0.5 mm away from the neuron. Two such rings,
with centers 0.5 mm apart — as from Yellow One and Two — have two intersections, just as in
that plane geometry exercise about bisecting a line.
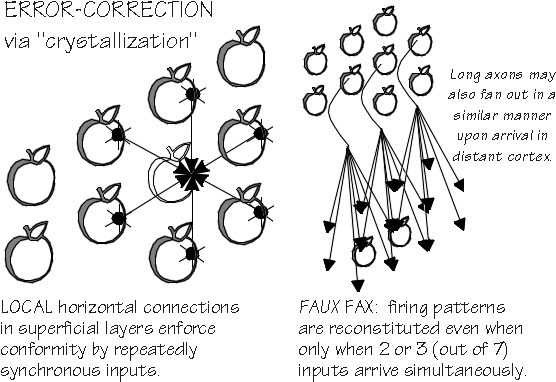
So it wouldn’t be surprising if Yellow One and Yellow Two, once they got their act in sync, managed to recruit a Yellow Four as well as a Yellow Three. And there are other neurons at the hot spot of the pair formed by One and Three: perhaps a Yellow Five will join the chorus, if it already has enough other inputs to put the paired inputs within range of its threshold. As you can see, there is a tendency to form a triangular array of often-synchronized neurons that could extend for a few millimeters across the cortical surface. Because one neuron can become surrounded by six others, all telling it to fire at a certain time, we have error correction: even if a neuron tries to do something different, it is forced back to the choral pattern that has become established by its insistent neighbors. That is essentially an error-correction procedure, just what the faux fax needs — if only the long corticocortical axon terminals did what the local ones do: fan out into patches about 0.5 mm apart rather than ending in a point. And they do fan out in a patchy manner — in about the right ballpark.
|
|
How big might an array become? It might be confined to its original Brodmann area, if the
skip spacing changed at the boundary. For example, in primary visual cortex, the skip spacing in
monkeys is 0.43 mm, and next door in the secondary visual area it’s 0.65 mm; recruiting across
the boundary might not work; but that’s an empirical question — we’ll just have to see. And
recruiting more neurons into the triangular array requires candidates that are already mildly
interested in the banana. So the triangular array of Yellows might not be too much larger than the part of the visual cortex receiving the image of the yellow banana. The neurons sensitive to line orientation might have been doing to same thing, too: several getting in sync, recruiting a chorus of the predisposed, and so forming another 0.5-mm triangular array centered elsewhere. For each separately-detected feature of the banana, there would be a different triangular array — and not necessarily extending the same distances across the cortex. Looking down on the flattened cortex (and assuming that a minicolumn lights up when an impulse fires), we would see a lot of flickering lights. If we restricted our field of view to a 0.5 mm circle, we would be unlikely to see much synchrony, just one of the Yellows firing a few times a second, one of the Lines firing a dozen times a second, and so on. But if we broadened our field of view to several millimeters, we would see a half-dozen spots lighting up at once, then another group lighting up. Each specialty has its own triangular array; taken together, the various arrays constitute a Banana Committee. Note that the original committee of Yellows and Lines might have been larger than 0.5 mm across, back before recruitment began to fill in things. Even if the original committee was scattered over a few millimeters, the triangular arrays serve to create a unit pattern that is much smaller (and potentially easier to recreate, when recalling the pattern). We have, in effect, compacted the code into a smaller space than it originally occupied, as well as making redundant copies. That has some interesting implications.
|
|
This is a spatiotemporal pattern having something to do with a banana’s representation, but
is it the cerebral code for banana? I’d call that the smallest such pattern that didn’t omit anything
important — the elementary pattern from which the triangular arrays of Lines and Yellow could
be recreated. If we zoom in, shrinking our field of view of the flickering minicolumns, what area will it cover at the point where we can no longer find synchronized minicolumns? Yes, it’s about 0.5 mm, but it isn’t a 0.5 mm circle — it is a hexagon that is 0.5 mm across between parallel faces. This is a simple matter of geometry: corresponding points (say, the upper right corners) of hexagonal tiles form triangular arrays. Anything larger than that hexagon will start including some redundant points that are already represented by another of their triangular array (and we’d sometimes see two synchronized points in our restricted view of view). The elementary pattern wouldn’t usually fill the hexagon (I imagine it as a dozen minicolumns active, out of a hundred or more in the hexagon — but the rest have to stay silent in order not to fog the pattern). We wouldn’t be able to see the boundaries outlined — so that we wouldn’t see a honeycomb when we looked down on the cortical surface while a territory was being cloned. Indeed, when wallpaper designers create a repeating pattern, they often make sure that the pattern unit’s boundary cannot be easily detected, so that the overall pattern will appear seamless. Though the triangular arrays do the recruitment and create the compact pattern, it is as if hexagons were being cloned. The triangular synchronicity doesn’t necessarily last for very long — it’s an ephemeral form of organization, and it might be wiped out during certain phases of an EEG rhythm associated with decreases in cortical excitability. If we want to recreate a spatiotemporal pattern that has died out, we could get it started from within two adjacent hexagons — indeed, from any two adjacent hexagons that the extended banana mosaic covered originally. It wouldn’t have to be the original pairs. The memory trace — the essential bumps and ruts for resurrecting the spatiotemporal pattern — could be as small as the circuitry in two adjacent hexagons. So repeated copying of the minimal pattern could colonize a region, rather the way that a crystal grows or wallpaper repeats an elementary pattern. If the melody recurred enough times before it stopped, LTP might linger in such a way that the spatiotemporal pattern was easily restarted, at one place or another. If the spatial pattern was relatively sparse, several cerebral codes (say, the ones for Apple and Tangerine) could be superimposed to give you a category, such as Fruit. If you tried superimposing several letters from a dot-matrix printer, you’d get a black mess. But if the matrix is sparsely filled, you can probably recover the individual members, because they each produce such distinctive spatiotemporal patterns. So this type of code could also be handy for forming categories that could be decomposed into examples, just as superimposed melodies can often be heard individually. Thanks to the telecopying aspect, you could form multimodal categories — such as all of the connotations of comb. My friend Don Michael suggests that meditation might correspond to creating, via a mantra, a large mosaic of a nonsense code, one without significant resonances or associations. If you maintained it long enough to wipe the slate clean of cares and preoccupations, allowing those short-term ruts to fade, it might give you a fresh start in accessing long-term memory ruts without getting hung up on short-term concerns.
|
|
There are some attractive features to what emerges from this analysis of the superficial
pyramidal neurons: Donald Hebb would have loved it, because it shows how some of the most
puzzling features of short- and long-term memory might be explained with cell assemblies (the
memory trace is stored in a distributed way, with no one site crucial for its recall, and so forth).
The gestalt psychologists would have liked the way that it makes possible the comparison of
figure and ground by the triangular arrays potentially extending beyond the object boundaries, a
spatiotemporal pattern forming that represents the figure-ground combination, rather than just
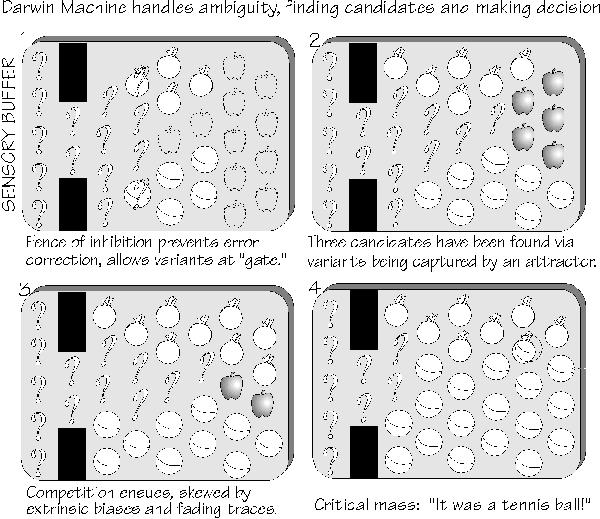
one or the other. And I like to think that Charles Darwin and William James would have liked the idea that mental life involves copying competitions biased by a multifaceted environment. Sigmund Freud might have been intrigued with the mechanism it suggests for how subconscious associations could occasionally pop into the foreground of consciousness. While I think that divergent thinking is the most important application of the neocortical Darwin Machine, let me first illustrate how it might work with a convergent thinking problem. Suppose that something whizzes past you and disappears under a chair. You thought it was round, and maybe orange or yellow, but it was moving very quickly, and now it’s out of sight, so you can’t get a second look. What was it? How do you guess, when the answer isn’t obvious? Your process first needs to find some candidates, then it needs to compare them for reasonableness. Happily, cloning competitions can do that. There’s a tentative cerebral code for the object, formed by all the feature detectors that it activated: color, shape, motion, and maybe the sound of it bouncing on the floor. This spatiotemporal pattern starts making clones of itself, in a manner of speaking.
Whether it can set up a clone next door depends on the resonances next door, those bumps in the road provided by the pattern of synaptic strengths and by whatever else is going on in the adjacent cortex. If you’d seen such an object many times before, there might be a perfect resonance — but you haven’t. Still, the tentative cerebral code has specialty components of Round, Yellow, Fast. Tennis balls have such attributes, and you have a good tennis ball resonance, so the adjacent area pops into the melody for Tennis Ball (a nice feature of chaotic attractors is that a near fit can be captured, transformed to the characteristic pattern). Cloning with poor resonances leads to dropouts of some components, so perhaps your Tangerine resonance captures a variant in another patch of cortex despite the color not being quite right.
|
|
What about cloning competitions? Here we have Unknown, Tennis Ball, and Tangerine
cerebral codes cloning away. Perhaps Apple pops out as well: if you saw someone eating an
apple a few minutes ago, there would be temporary ruts for Apple, because of the NMDA
synapses that were strengthened in that pattern. But then Apple is overrun by the Tangerine
pattern, which is cloning away. Over on the other side of Unknown’s current territory, Tennis
Ball is doing quite well and eventually it overrides and replaces Unknown, even encroaching on
Tangerine’s territory. At about this time, you say, “I think that was a tennis ball,” because there
were finally enough clones in the Tennis Ball chorus to get a coherent message through to your
left-lateral language cortex, over the corticocortical pathways from the occipital lobe to the
temporal lobe. Something else happens now: a new spatiotemporal pattern starts cloning through the work space; this time, you see something very familiar (the chair) and a critical chorus of Chair is quickly established without any real competition, because the sensory spatiotemporal pattern hits instantly on a resonance before any variants have time to get going. The NMDA synapses used in the Tennis Ball and Tangerine patterns are still jazzed up, however, and for another five minutes it will be easier than usual to recreate either of these spatiotemporal patterns in the parts of the work space that they last occupied. Perhaps Tangerine continues to clone and make mistakes, hitting upon the Orange Fruit resonance — so that a minute later, you wonder if you were wrong about that tennis ball. That’s how it could happen — how I imagine that our subconscious processes sometimes come up with someone’s name a half hour too late. The pattern resonances are not unlike how we imagine locomotion to work in the spinal cord: there’s a connectivity — all those synaptic strengths between the various neurons — and given certain initial conditions, you can pop into the resonance for the spatiotemporal pattern that implements Walk. With other initial conditions, you pop instead into Jog, Lope, Run, or Hopscotch. In the sensory cortex, you may pop into Orange or Tangerine even when you see fruit that is neither. As I mentioned in chapter 5, categories are why the Japanese have so much trouble with English L and R sounds: both are captured by their mental category for a particular Japanese phoneme. Reality is quickly replaced by mental models. As Henry David Thoreau said, “We hear and apprehend only what we already half know.” The cortex is in the business of quickly learning new patterns, whether sensory or movement, and creating variations on them. The variations allow for competitions to determine what pattern best resonates with the connectivities, and these in turn are often biased by a number of sensory inputs and emotional drives.
|
|
Relationships, too, can be coded by spatiotemporal patterns — just as well sensory or
movement schemas are. Just combine codes to make a new arbitrary pattern, just as a left-hand
rhythm can be superimposed on a right-hand melody. The lingua ex machina of chapter 5 offered some specific examples of what fancy relationships (as in a sentence) might involve — all those obligatory and optional roles. Those obligatory arguments of a verb such as give are about relationships, and cognitive dissonance results when an obligatory role goes unfilled (as, alas, advertising agencies have discovered; Give Him forces you to read the billboard again to see what you missed, and thereby remember the ad better). So, is a sentence simply one big spatiotemporal pattern, cloning away in competition with other sentence codes? Not necessarily. We don’t require copying competitions in order to make a decision; simple rating schemes ought to suffice, if nothing particularly new is involved. Recall the cormorant of chapter 2: rating schemes will do for its decision making, because the choices (swim, dive, dry wings, fly away, look around a little longer) are already well-shaped by evolution over the generations. Copyable schemas aren’t everything, once you get close enough to standard meanings.
|
|
The superficial cortical layers in many primates have the standard-skip wiring that predicts
the ephemeral triangular arrays. It is not known how often any animal uses this wiring for
cloning wallpaperlike hexagonal patterns; perhaps it only happens briefly, during prenatal
development — as a sort of test pattern that guides use-dependent connections — and never occurs
again. Or perhaps some areas of cortex are committed to full-time specialization and never clone
such ephemeral patterns, while other areas often support sideways copying and become erasable
workspaces for darwinian shaping-up processes. Since clones of movement commands would be
particularly useful for throwing — they can reduce timing jitter — perhaps there was some natural
selection for big work spaces in the hominid evolution of throwing accuracy. They’re all
empirical questions. Once we have improved the resolution of our recording techniques, we’ll
have to see where hexagonal cloning lies on the spectrum of possibilities. But something very close to such cloning competitions is needed to satisfy the essentials for the Darwin Machine — that’s the real reason why I’ve led the reader through this cortical maze. Here, at least, we have 1) a distinctive pattern, 2) copying, 3) variation, 4) possible competitions for work spaces, 5) multifaceted environments (both current and memorized) to bias the competition, and 6) a next generation more likely to have variants established from the clones with the biggest territories (big territories have more perimeter, which is where variants can escape error correction tendencies and get started cloning their new pattern). In a longer book about the neocortical Darwin Machine itself (The Cerebral Code), I’ll explain all about the spice and speed that you’d get from cerebral analogues of sex, islands, and climate change. And speed we need, if a darwinian process in the brain is to work fast enough to provide our guessing-right intelligence.
We keep trying to carve up the cerebral cortex into specialized “expert” modules. It’s a good research strategy, to look for specialization, but I don’t take it seriously as an overview of how the association cortex works. We need some erasable work spaces, and we need to be able to recruit helpers for difficult tasks. That suggests that any “expert” modules are also generalists — as when a neurosurgeon acts as a paramedic in an emergency. One of the things I like about the ephemeral hexagonal mosaic is that it suggests a resolution of the expert-generalist dilemmas: even a cortical area with “expert” long-term ruts could serve as a work space, using overlaid short-term ruts to bias competitions. Such a mosaic also suggests a way that subconscious thoughts could meander and occasionally pop some relevant fact from the past into your stream of consciousness. Best of all, because variants themselves can clone their way to temporary success, the patchwork quilt is creative — it can be shaped up from humble beginnings into something of quality. Even higher forms of relationships, such as metaphor, seem likely to arise, because the cerebral codes are arbitrary and capable of forming new combinations. Who knows — perhaps by now you’ve even acquired a cerebral code for Umberto Eco’s Mac-PC analogy.
|
|
The synchronized triangular arrays with such interesting implications for darwinian copying
competitions turn out to have implications for fancy language as well, potentially giving intelligence a boost
from another direction. There is a considerable step up from protolanguage to our full-fledged syntactic language, yet linguistics researchers doubt that intermediate forms exist. Even when it has ample vocabulary, protolanguage has very little structure, relying mostly on simple contextual associations between a few words to convey the message. Adding structure makes a big difference. A brain mechanism for recursive embedding (such as sentences within sentences: I think I saw him leave to go home) is considered essential for Universal Grammar. Among the linguists’ other desiderata are mechanisms for long-range dependencies, including binding of pronouns to their referents. Such binding requires longer-than-local links; recursive embedding, moreover, requires structuring a hierarchy of them. Nonadjacent areas of cerebral cortex are likely to be involved in many attempted associations, given what we know about comb’s visual connotations being stored near visual cortex, its auditory aspects near auditory areas, and so forth. Yet corticocortical axon bundles are considerably worse than the incoherent fiber optic bundles, where neighbors fail to remain neighbors. Point-to-point mappings are also likely to be lost as each axon’s terminals fan out, not unlike the spread of a flashlight beam. Despite incoherence from both jumble and smear, some of the distorted patterns can presumably, with experience, be recognized at the far end, using cluster-analysis-like mechanisms analogous to those of categorical perception. This ought to allow the conveyance of well-practiced special cases, analogous to the mariners’ signal flags - though perhaps only a few at a time, thereby limiting the possible novel associations that could be conveyed between cortical areas. Embedding would be restricted to stock phrases. This incoherent level of corticocortical capability ought to be able to handle protolanguage. But the error-correction mechanism offers the possibility of sending arbitrary spatiotemporal patterns down the corticocortical bundle - and succeeding on the first try, so that one is no longer limited to the spatially and temporally distorted patterns that have been recognized by the target cortex as meaningful special cases. Such corticocortical coherence would mean that novel associations could be conveyed. Furthermore, the same spatiotemporal firing pattern would now be shared by both the source and the target area; the target cortex could send it back with similar error correction and have it automatically recognized in the source cortex, with no need to tune up to a doubly-distorted version and then construct an equivalence to the original spatiotemporal firing pattern. Back projections using the same code mean that you can have a distributed choir, distant chorus members contributing to keeping its membership above a critical size. A backprojected song might not need to be fully featured to help out with the chorus. It could be more like that sing-along technique where a single voice monotonically prompts the next verse and the audience repeats it with musical elaborations. Back projections also provide an audit trail that can resolve ambiguity. ("Who said X? Sing it again, the whole thing!") With links that can maintain sentence structure, embedding becomes possible: no longer is there a danger that the mental model of the eight-word amalgamation the tall blond man with one black shoe will be scrambled into a blond black man with one tall shoe. Corticocortical precision per se is thus one candidate for the big step up from protolanguage to Language (though you still need lots of little rules at the level of argument structure). Indeed, the transition to arbitrary code conveyance could have implemented two major innovations of Universal Grammar - embedding and long-range links - in one step. So we now have several candidates, Darwin Machines and coherent corticocorticals, for what might have boosted intelligence and language, enabling the infrequently-innovating Homo erectus cultures to evolve, about 250,000 years ago, into the constantly-changing cultures of Homo sapiens.
|
 You are reading HOW BRAINS THINK.
You are reading HOW BRAINS THINK.
The paperback US edition |