William H. Calvin, "Error-correcting Codes" (1993)
Error-correcting Codes:
Coherent Hexagonal Copying from Fuzzy Neuroanatomy
WILLIAM H. CALVIN
Department of Psychiatry and Behavioral Sciences,
University of Washington
Seattle, Washington 98195-1800 USA
WCalvin@U.Washington.edu
Calvin, William H. (1993). Error-correcting codes: Coherent hexagonal copying from fuzzy neuroanatomy. World Congress on Neural Networks 1:101-104 (1993).
Copyright 1993 by W. H. Calvin.

ABSTRACT
Fuzzy approximations to a point-to-star wiring principle for
recurrent excitation can clone spatial patterns of activity.
Because of temporary entrainment of otherwise active neurons,
the homologous points form a triangular mosaic of synchronized
neurons. The largest such collection of points that can be so
copied without screen-wrap-like overwriting is a hexagon as
wide as the point-to-star distance (about 0.5 mm in the case
of pyramidal neurons of the superficial layers of primate
neocortex). This hexagonal spatiotemporal neuron firing
pattern becomes a candidate for a cerebral code that can
represent a mental image in the same manner as a barcode
represents the contents of a grocery package. This pattern
may clone considerable territories, with conformity enforced
as a variant point becomes surrounded by up to six identical
homologous points. If the long corticocortical bundles
approximate the same point-to-star principle as the local
connectivity, long-distance copying becomes possible without
the point-to-point mapping achieved by a coherent light pipe,
as the parent pattern can seed a mosaic of the same pattern at
a distant cortical site.
Since Hebb's 1949 cell-assembly proposal1, we have realized
that evoking a memory could involve an ensemble of cortical
neurons, each of which helps to implement other memories as well.
Different schemas might be characterized by different firing
patterns in time and space. The analogous problem in genetic
memory, that of the genetic code, was solved by first identifying
which physical patterns could be reliably copied. But copying
has not been on the neurophysiological agenda; we usually assume
transformations rather than cloning when information is moved.
Many movement command clones were, however, inferred2,3 from
the need to reduce timing jitter during precision throwing. And
the notion of convergence zones for associative memories4 raises
the issue of maintaining the identity of a cerebral code during
long-distance corticocortical transmission, such as through the
corpus callosum. Because of the reciprocal connections between
distant cortical regions, any distortions of the original
spatiotemporal firing pattern during forwards transmission would
need to be compensated during reverse transmission in order to
maintain the pattern as the local code for a sensory or motor
schema. Here I suggest an error-correction mechanism in both
directions that avoids the need for an inverse transform.
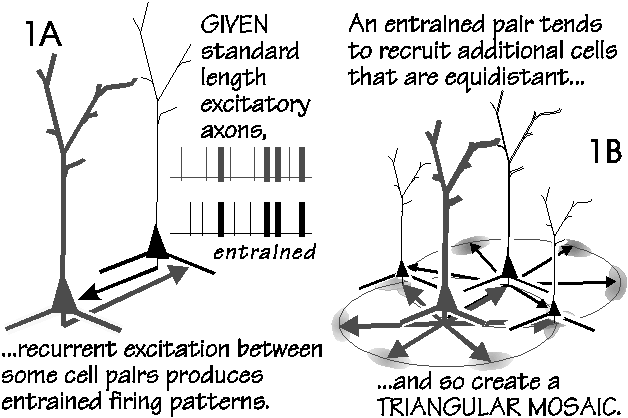
Entrainment via Minor Recurrent Excitation
The average cortical neuron contacts fewer than 1 percent of
the neurons within a 1 mm radius5. One wiring principle can be
seen from the axons of pyramidal neurons in the superficial
cortical layers6,7,8. An axon goes a characteristic lateral
distance without any terminations, then it produces a tight
cluster (it may continue for an identical distance and then
produce another cluster, though this will not be addressed here).
J. S. Lund (personal communication) estimates this gap as about
0.5 mm in visual areas, 0.7 mm in prefrontal cortex, and nearly
1.0 mm in motor cortex of monkeys. The synapses are excitatory
and often onto cells of the same type9. Because of the standard
axon length (hereafter, simply 0.5 mm), recurrent excitation
becomes possible.
Even if the synaptic strengths were high, much longer axons are
required for a reverberating loop. But even weak coupling
between relaxation oscillators is known to produce
entrainment10,11, and that is the feature utilized here. Were
the cells otherwise active, they would soon tend to produce some
spikes at about the same time (Fig. 1A). This intermittent
synchrony12 suggests the entrainment of other superficial
pyramidal neurons located at the two points which are equidistant
from the first pair (Fig. 1B).
If sufficient axons traveled in approximately the right
directions (up to six, at 60deg angles from a point), this
recruitment could continue to eventually form a mosaic of
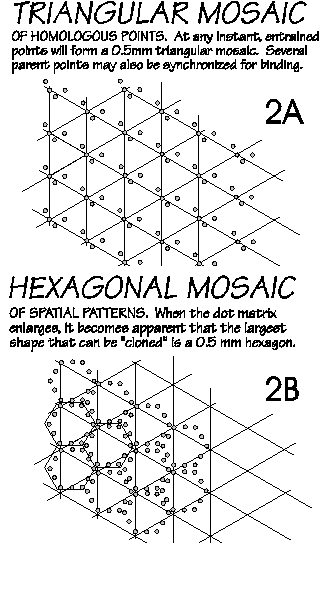
synchronous activity at 0.5 mm spacings (Fig. 2A). While the
most efficient anatomy would be six equally-spaced axon branches
from the same cell (Fig. 1B, Fig. 3AB), a more general wiring
principle would be enough neighboring work-alike neurons to
collectively send axons in all directions and thereby create an
annulus of excitation. Cells in cortical minicolumns are often
interested in the same kinds of stimuli (orientation columns) and
fire in synchrony (at least in development); since there are
about 100 neurons in such a column, coverage may well be
sufficient without individual axons being able to branch at 60deg
angles. Because simultaneous arrivals at the outlying neuron are
the actual criterion rather than equal length, the standard axon
can vary so long as conduction velocity or synaptic delay is
tuneable. Thus fuzzy anatomy, so long as the 60deg directions are
not avoided, can yield a self-organizing triangular mosaic.
The largest copyable pattern is
a 0.5 mm hexagon (Fig. 2B).
Concurrent nonhexagonal
activities may well be
compatible, especially in other
cortical layers. Indeed,
something needs to get the cells
firing so that weak coupling can
entrain them (this also suggests
that mosaics can be erased with
diffuse waves of inhibition).
Note that hexagons are not an
assumption: they are an emergent
property of standard axon lengths
and weak excitatory coupling that
entrains.
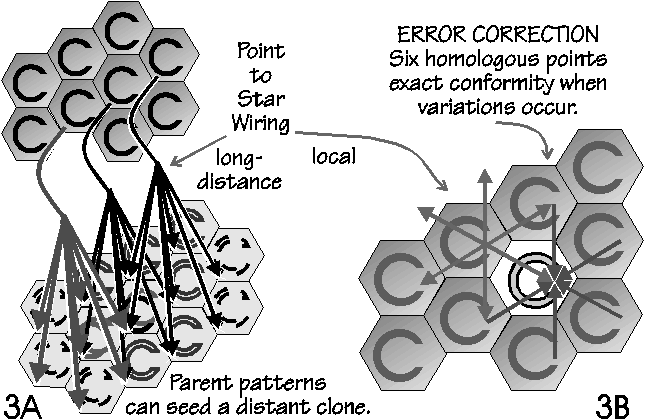
Error-correction tendencies
Like a crystal in formation, a
neighborhood of hexagons will
tend toward conformity (Fig. 3B)
because any deviating point
repeatedly receives synchronous
inputs from six homologous
points.
The same fuzzy point-to-star
wiring as used locally (Fig. 3B)
could also operate over long
corticocortical paths (Fig. 3A).
While some inputs will go astray
via topographic mapping errors or
temporal dispersal, only several
repeatedly synchronous inputs
might be needed to entrain the
activity of the distant neurons;
these coherent inputs could come from any of seven (center plus
six neighbors) distant points. While point-to-star will not copy
spatially unorganized activity in the manner of a coherent light
pipe, it does allow a chorus to recreate their common pattern
among a few distant listeners, that then clone their own
territory.
Two hexagonal patterns could be superimposed, via either local
or long-distance copying, and so form a new category, an episodic
memory, or an association between a sensory schema and a response
schema. If the dot matrix is sparsely populated (and estimates
suggest that a dozen minicolumns might be active, out of 300 in
the hexagon), the composite could serve as a form of associative
memory in the manner of a double exposure. I discuss
elsewhere13 the implications of hexagonal copying competitions
for implementing a msec-to-minute version of the same darwinian
process familiar from the immune response and species evolution.
Neurallike networks could also 1) use hexagonal dot-matrix
patterns as item representations, could 2) form associations, and
3) so implement a novel computing architecture with wiring that
is diffuse enough to perform multiple tasks.

References
1. Hebb, D.O., The Organization of Behavior (Wiley, New York,
1949).
2. Calvin, W. H., J. Theor Biol. 104, 121-135 (1983).
3. Calvin, W. H., The Cerebral Symphony(Bantam, New York, 1989).
4. Damasio, A.R., Cognition 33, 25-62 (1989).
5. Stevens, C. F., Neural Computation 1, 473-479 (1989).
6. Katz, L.C., Callaway, E.M., Ann. Rev. Neurosci. 15, 31-56(1992).
7. Rockland, K.S., Lund, J.S., Science 215, 1532-1534 (1982).
8. Gilbert, C.D., Hubel, D.H., J. Neurosci. 3, 1116-1133 (1983).
9. White, E.L., Cortical Circuits: Synaptic Organization of the
Cerebral Cortex Structure, Function, and Theory (Birkhauser,
Boston, 1989).
10. Winfree, A. T., The Geometry of Biological Time (Springer
Verlag, Berlin, 1980).
11. Somers, D., Kopell, N., Biol. Cybernetics (in press, 1992).
12. Engel, A.K., Koenig, P., Kreiter, A.K., Schillen, T.B.,
Singer, W., Trends Neurosci. 15, 218-226 (1992).
13. Calvin, W. H., Soc. Neurosci. Abstr. 18, 214.18 (1992)

Click here to send E-mail WCalvin@U.Washington.edu
Mailing address: University of Washington, Seattle WA 98195-1800 USA.
A list of my other books and articles can be found here.
[Jump to Top]
Revised 23 September 1995
WHC
![]()


